Wie stabil sind Konstruktionsprofile?

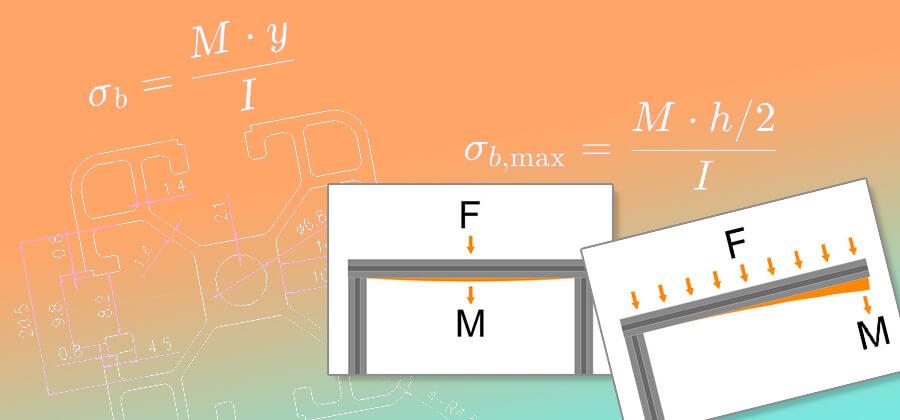
Schritt für Schritt erklärt, wie man berechnet ob ein Konstruktionsprofil eine Last tragen kann oder darunter dauerhaft verformt.

Wann führt eine Last zur dauerhaften Verformung

Das Konstruktionsprofile bei einer Belastung durchbiegen ist vollkommen logisch. Wie stark diese Durchbiegung ausfällt, ist im Wesentlichen vom Profil und dessen Länge, dem Eigengewicht, dem zusätzlichen Gewicht, der Lastverteilung und der Montageart abhängig. Die Formeln zur Berechnung der Durchbiegung wirken auf den ersten Blick sehr komplex. Darum haben wir diesem Thema einen gesonderten Blogbeitrag gewidmet, in dem wir jeden einzelnen Parameter und die Berechnung in kleinen, verständlichen Einzelschritten erklären. Doch wann ist diese Belastung zu hoch? Wann hat das Gewicht Auswirkungen auf eine dauerhafte Verformung? Mit dieser Fragestellung werden wir uns in diesem Beitrag ausführlich befassen.

Erst mal etwas zur Theorie der Biegespannung

Um die Biegespannung, also die mechanisch auf das Material einwirkende Spannung durch Belastung, zu berechnen, müssen wir wissen, wie stabil das Material ist. Hier ist ein Blick in das Datenblatt des Werkstoffs hilfreich, denn wir müssen den Wert der Streckgrenze R_e (welche gerne auch Streckspannung oder Fließgrenze bezeichnet wird) ermitteln. Dieser kann von Werkstoff zu Werkstoff sehr stark variieren. Selbst bei einem Konstruktionsprofil aus Aluminium ist ein genauer Blick wichtig, denn Alu ist nicht gleich Alu. Hier ist die konkrete Legierung von Bedeutung, um die Fließgrenze zu ermitteln.

Die Fließgrenze eines Materials beschreibt die Spannung, ab der es plastisch verformt wird, also das Material beginnt, sich dauerhaft zu verformen, ohne wieder in seine ursprüngliche Form zurückzukehren, wenn die Belastung entfernt wird. Sie ist somit eine wichtige mechanische Eigenschaft, die angibt, wie viel Spannung ein Material aushalten kann, bevor es beginnt, sich dauerhaft zu verformen und wird, ähnlich wie das Elastizitätsmodul als weitere wichtige physikalische Größe, in Pascal oder N/mm² angegeben. Für Aluminium bezeichnet die Fließgrenze den Punkt, an dem es von der elastischen Verformung (die reversibel ist) in die plastische Verformung (die irreversibel ist) übergeht. Dies bedeutet, dass das Aluminiumprofil beim Überschreiten der Fließgrenze eine dauerhafte Verformung durch Dehnung erfährt. Bei unseren Konstruktionsprofilen kommt eine hochwertige EN AW 6063 T5 Aluminium-Legierung mit einer Streckgrenze von sagenhaften 292MPa zum Einsatz. MPa lässt sich dabei durch die Einheit N/mm² austauschen, was auch die Einheit der Biegespannung unter Lasteinwirkung entspricht und sich somit leichter vergleichen lässt.

Ein weitere wichtiger Wert ist das Widerstandsmoment eines Querschnitts, der bei unseren Konstruktionsprofilen sowohl für die X- als auch die Y-Achse gleich ausfällt, da die Profilkonstruktion symmetrisch ist. Das Widerstandsmoment ist dabei immer spezifisch auf den Profilquerschnitt bezogen.

Das Widerstandsmoment W unserer Konstruktionsprofile

• Konstruktionsprofil 20x20, Nut6:Widerstandsmoment W_x, W_y: 0,71cm³
• Konstruktionsprofil 30x30, Nut8:Widerstandsmoment W_x, W_y: 1,57cm³
• Konstruktionsprofil 40x40, Nut8:Widerstandsmoment W_x, W_y: 3,58cm³

Neben den physikalischen Daten benötigen wir nun noch das Gewicht, welches auf das Profil einwirkt. Die Länge des Profils müssen wir ebenfalls wissen, denn ein längeres Profil wird unter diesem Gewicht einen höheren Wert zur Biegespannung aufweisen, als ein gleiches Profil in kürzerer Ausführung. Zu guter Letzt spielt auch die Art der Montage und die Lastverteilung eine Rolle. Das diese Parameter mitunter deutliche Auswirkung auf die Belastbarkeit eines Konstruktionsprofils haben, haben wir in den Erläuterungen zur Berechnung der Durchbiegung ja schon verdeutlicht.

Berechnen der Biegespannung - so wirds gemacht!

Parameter zur Berechnung der Biegespannung σ_b

• M Das Biegemoment in N*mm des Lastfalls
• W Das Widerstandsmoment des Profilquerschnitts in mm³

Allgemeine Biegespannungsformel

${\sigma }_{\mathrm{b}}=\frac{M}{W}$

Das Biegemoment M hängt von der Last F und der Länge L des Profils ab. Ob es sich bei der Last um eine gleichmäßig verteilte Last oder eine punktuelle Lasteinwirkung handelt, ist für die Ermittlung ebenso von Bedeutung, wie die Montageart, denn daraus leiten sich jeweils sogenannte Lastfälle mit unterschiedlichen Formeln und konstanten Faktoren zur Berechnung des Biegemoments ab. Das Biegemoment eines bestimmten Lastfalls ist aber ein wesentlicher Bestandteil der Formel zur Berechnung der Biegepsannung.

Die Last F ist eine Kraft die in Newton (N) angegeben wird. Diese wird durch eine einfache Multiplikation der Masse m, also dem Gewicht (kg), welches auf das Profil einwirkt und der Gravitationskonstante g berechnet. Diese hat auf der Erde einen Wert von ca. 9.81kg*m/s² und wird im allgemeinen Sprachgebrauch auch als Erdanziehungskraft bezeichnet. Die Formel zur Umrechnung der Gewichtsbelastung F haben wir im Blogartikel zur Berechnung der Durchbiegung genau erklärt. Dort ist auch die Formel zur Berechnung der Flächenlast q bei gleichmäßiger Lastverteilung detailliert beschrieben.

Das Biegemoment M für Lastfälle bei beidseitiger Montage des Profils

Die Formel für das Biegemoment bei gleichmäßiger Lastverteilung q

$M=\frac{q*L^2}{8}$

Die Formel für das Biegemoment durch Gewichtsbelastung F bei zentriert wirkender Last

$M=\frac{F*L}{4}$

Das Biegemoment M für Lastfälle bei einseitiger Montage des Profils

Die Formel für das Biegemoment bei gleichmäßiger Lastverteilung q

$M=\frac{q*L^2}{2}$

Die Formel für das Biegemoment durch Gewichtsbelastung F am Ende des offenen Profils

$M=F*L$

Ein Praxisbeispiel zur Berechnung der Biegespannung

Angenommen, wir wollen einen Bulli ausbauen und auf der Ladefläche ein Bettgestell aus Konstruktionsprofilen errichten. Dazu setzen wir Konstruktionsprofile in 40x40mm mit 8mm Nut in einer Länge von 2 Metern für die lange Seite ein, die an beiden Seiten fest an den Stützpfosten montiert werden. Das zu erwartende Gewicht, welches auf das Profil wirken wird, besteht aus der Summe der Einzelgewicht von Matratze, Lattenrost, Bettwäsche und dem eigenen Körpergewicht, so dass wir hier eine Gesamtmasse von 100kg annehmen. Normalerweise liegen wir im Bett, so dass wir von einer verteilen Gewichtsbelastung ausgehen können, aber manchmal sitzt man auch mittig auf dem Bett, wodurch wir zudem eine gemischte Lastwirkung erhalten. Daher gehen wir auf Nummer sicher und berechnen weiter unten noch die Biegespannung für eine zentriert wirkenden Punktlast.

Gegebene Parameter zur Berechnung der Biegespannung σ_b

• Profillänge L: 2.000mm
• Masse der Belastung m: 100kg
• Widerstandsmoment des Profils W: 3,58cm³
• Streckgrenze des Profils R_e: 292MPa (oder N/mm²)
• Lastfall: Beidseitig gelagerter Balken mit gleichmäßig verteilter Last q

Zu allererst rechnen wir die Masse von 100 Kilogramm in die Kraft in Newton um.

$F=100\mathrm{kg}*\mathrm{9,81}\frac{m}{s^2}=981\mathrm{kg}*\frac{m}{s^2}\approx 981N$

Nachdem die Kraft von 981 Newton bekannt ist, werden wir diese zur Berechnung der Flächenlast nutzen, die für die Berechnung der Biegespannung bei gleichmäßig verteilter Lasteinwirkung benötigt wird. Für die Biegespannung bei zentriert wirkender Last, können wir die eben errechnete Kraft direkt verwenden.

$q=\frac{981N}{2.000\mathrm{mm}}=\mathrm{0,4905}\frac{N}{\mathrm{mm}}$

Unsere Berechnung zeigt, dass bei einer Kraft durch Gewichtsbelastung von 981 Newton auf jeden Millimeter eines Profils eine Kraft von 0,4905 Newton wirkt. Diesen Wert nutzen wir nun zur Berechnung des Biegemoments.

$M=\frac{\mathrm{0,4905}\frac{N}{\mathrm{mm}}*(2.000\mathrm{mm}{)}^2}{8}=\frac{\mathrm{0,4905}\frac{N}{\mathrm{mm}}*\mathrm{4.000.000}{\mathrm{mm}}^2}{8}=\frac{\mathrm{1.962.000}N*\mathrm{mm}}{8}=245.250N*\mathrm{mm}$

Nun folgt der letzte Schritt. Wir berechnen die Biegespannung. Allerdings müssen wir hier auch darauf achten, dass die Streckgrenze meist in cm³ angegeben wird, welche wir für gleiche Maßeinheiten in mm³ umrechnen müssen. Das ist aber sehr einfach, denn ein Kubikcentimeter ist 1cm*1cm*1cm oder im Millimeter ausgedrückt 10mm*10mm*10mm, was 1000mm³ entspricht.

${\sigma }_{\mathrm{b}}=\frac{245.250N*\mathrm{mm}}{\mathrm{3,58}{\mathrm{cm}}^3}=\frac{245.250N*\mathrm{mm}}{3.580{\mathrm{mm}}^3}==\mathrm{68,5055866}\frac{N}{{\mathrm{mm}}^2}$

Da der Wert der Biegespannung von gerundet 68,5N/mm² deutlich unter der Streckgrenze des verwendeten Aluminiums mit einem Wert von 292N/mm² liegt, ist eine dauerhafte Verformung bei gleichmäßig verteilter Belastung mit einem Gewicht von 100kg nicht zu befürchten.

Gegebene Parameter zur Berechnung der Biegespannung σ_b

• Profillänge L: 2.000mm
• Gewichtslast F: 981N
• Widerstandsmoment des Profils W: 3,58cm³
• Streckgrenze des Profils R_e: 292MPa (oder N/mm²)
• Lastfall: Beidseitig gelagerter Balken mit zentriert wirkender Last F

Nachfolgend berechnen wir die Biegespannung, wenn das Gewicht zentriert als Punktlast auf die gleiche Konstruktion wirkt. Das ist die maximale Belastungsart, die auf ein beidseitig montiertes Profil einwirken kann. Dies ist für unser Beispiel zwar nicht ganz zutreffend, da mindestens das Lattenrost und die Matratze als verteilte Last zu verstehen sind, aber wenn wir das mal außen vor lassen ergibt sich ein sehr guter Anhaltspunkt, der Aufschluss darüber gibt, ob die Konstruktion unter der Lasteinwirkung dauerhaften Schaden durch Verformung nimmt, oder diese bedenkenlos tragen kann.

${\sigma }_{\mathrm{b}}=\frac{981N*2000\mathrm{mm}}{4*\mathrm{3,58}{\mathrm{cm}}^3}=\frac{\mathrm{1.962.000}N*\mathrm{mm}}{4*3.580{\mathrm{mm}}^3}=\frac{\mathrm{1.962.000}N*\mathrm{mm}}{14.320{\mathrm{mm}}^3}==\mathrm{137,011173}\frac{N}{{\mathrm{mm}}^2}$

Auch bei zentrierter Lasteinwirkung mit vollem Gewicht von 100kg ergibt sich eine Biegespannung von gerundet 137N/mm², der unterhalb der Streckgrenze des Aluminium-Profils liegt. Erst bei einem Gewicht von mehr als 213kg ist mit einer irreversiblen Verformung des Profils anhand der Materialeigenschaften der verwendeten Aluminium-Legierung und des vorliegenden Profilquerschnitts zu rechnen.

Wir hoffen, dass die Erläuterungen zur Berechnung die Biegespannung unserer Konstruktionsprofile hilfreich und leicht verständlich sind. Die Formeln im Beitrag beziehen sich zwar auf unsere Profile, können aber durchaus auch für andere Werkstoffe wie Holzbalken oder Kunststoffplatten eingesetzt werden, wenn man die entsprechenden Werte für Streckgrenze und Widerstandsmoment vom gewünschten Material kennt und in die Formel einsetzt. Die Angaben sind im Regelfall unter den technischen Daten im Bereich der mechanischen Werkstoffeigenschaften in den Datenblättern der Hersteller aufgeführt.

Wenn Ihr immer auf dem Laufenden bleiben wollt, wissen wollt, was uns bewegt und was sich alles in unserem Onlineshop tut, folgt uns doch auf Instagram und Facebook. Wir freuen uns über jedes Like.

Euer Sascha von S-Polytec